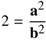Starting in the 6th century BC, a group of Greek philosophers, now known as the pre-Socratics, began to produce an avalanche of new ideas that would change the world forever.
Dissatisfied with invoking the Olympic gods to explain the world, they began to look for naturalistic explanations. Some hypothesized that the world was made of various elements, while others claimed it was composed of bouncing atoms. Pythagoras famously discovered music had a mathematical foundation, giving him the idea that perhaps mathematics itself was at the root of the universe.
Over a number of centuries, they produced some of the greatest intellectual achievements of humanity. Thales became the first to provide a formal proof of a mathematical theorem, Aristotle discovered formal logic and gave various proofs for the spherical shape of the Earth, Eratosthenes measured the circumference of the Earth with remarkable accuracy, and Ptolemy created an accurate model of the motion of the planets.
Starting in the 6th century BC, a number of philosophers began to seek a physical explanation of the universe. Today, these philosophers are called the pre-Socratic philosophers, but Aristotle referred to them as physiologoi (“natural philosophers”), distinguishing them from the earlier theologoi (“theologians”) and mythologoi (“storytellers”), who both attributed natural phenomena to the gods. The earliest known Greek thinker to inquire into the physical workings of the universe was Thales (624–545 BC), a merchant from the Greek colony Miletus, on the west coast of Turkey. As a merchant in this multicultural city on the edge of Asia, he must have had contacts introducing him to the knowledge of the civilizations of the Middle East and Egypt. As with many early Greek thinkers, we only know about his work through summaries in secondary sources. Both Aristotle and Herodotus agree that Thales used logic to understand the physical universe. He developed a belief still central to modern science, namely that despite the wide variety of phenomena around us, the universe is, in essence, an orderly place that operates on a few basic naturalistic mechanisms. This attempt to reduce the complexity of the world is now called reductionism. This idea turned the study of the universe from an attempt to understand the will of the gods into a rudimentary form of science. Aristotle also credited him with the pursuit of knowledge for its own sake. He wrote:
They were pursuing science in order to know, and not for any utilitarian end. […] It was when almost all the necessities of life […] had been secured, that such knowledge began to be sought. […] It is owing to their wonder that men […] began to philosophize. They wondered […] about the phenomena of the moon and those of the sun and of the stars, and about the genesis of the universe. [109]
By presenting logic as the ultimate tool to understand the universe—as opposed to receiving knowledge through divine revelation—Thales inadvertently placed humanity on a pedestal, placing great trust in the capacity of the human mind. This became the central idea of Greek philosophy. Aristotle made it explicit by stating that reason was man’s most defining characteristic:
All men by nature desire to know.
Thales’s execution of these principles, however, was rather simplistic. He observed that water existed as a solid, a liquid, and a gas. He also noticed that water was essential to life. From these observations, he erroneously concluded that “everything is made of water.”
Perhaps surprisingly, his materialistic worldview did not make Thales an atheist. In fact, according to Aristotle, “Thales thought all things are full of gods.” In fact, most pre-Socratics retained some form of divinity, although their gods were generally more abstract than the traditional gods of Greece and they rarely required worship.
Following in the footsteps of Thales, many other philosophers attempted to discover the true building blocks of the universe. Heraclitus (535–475 BC) concluded the primary building block must be fire because, like everything in this world, it is constantly subject to change. Take, for instance, a river. Every time you step into a river, it is filled with different water. Therefore, he famously concluded:
No man ever steps into the same river twice.
Two other early influential naturalistic thinkers were Anaximander (c. 610–546 BC), a student of Thales, and his own student Anaximenes (c. 586–526 BC), both also from the city of Miletus. Whereas traditionally, Greeks believed thunder was caused by Zeus, Anaximander theorized it might be caused by wind colliding with clouds. He even claimed life originated in water and later evolved to land. Anaximenes explained the seasons based on the position of the sun in the sky, rainbows in terms of the effects of sunlight on clouds, and stars as burning pieces of material pushed upward on evaporated moisture. He explained earthquakes as caused by the drying of land, requiring no intervention by the “earth-shaker” Poseidon. As with Thales, Anaximander and Anaximenes did believe in gods. For Anaximander God was infinity and for Anaximenes it was the element air (which comes dangerously close to atheism).
Another naturalistic thinker was Anaxagoras (c. 510–428 BC). Anaxagoras suggested that earthquakes were caused by air escaping from cavities below the earth. He also called the sun a “glowing stone,” denying its divinity, for which he was put on trial for impiety and exiled. He was accused of being an atheist, although in reality he believed in a divinity called nous (“mind”), which he believed was unchanging and infinite and was behind every motion in the universe. Plato would later criticize him, stating that although he spoke of the divine nous, when it came down to it he only used materialistic explanations to explain the universe.
Empedocles (495–435 BC) tried to unify a number of earlier theories and concluded that the universe was built up out of four elements: water, fire, earth, and wind. Mixing these elements was believed to produce the complexity of phenomena we see in the world around us.
Around the year 500 BC, a man named Parmenides, from Elea, a Greek colony in Southern Italy, took reductionism to the extreme. Whereas Heraclitus had claimed that the world was in constant flux, Parmenides thought that change and motion were illusions. He believed that although we see things go in and out of existence, in reality, there is only one eternal and complete Being. This Being, according to Parmenides, is not subject to change and, as a consequence, the world cannot be subject to change either. Since our senses do perceive change, they must be unreliable and therefore cannot be trusted. Instead, he believed, we can only get to the truth through abstract reasoning.
Parmenides’s student Zeno (c. 490–430 BC) set out to prove that his master was right. In his first “proof,” he argued that an arrow in flight is, in fact, motionless. He reasoned that since, at each moment, the arrow occupies a space that is exactly equal to itself, it must, therefore, be at rest. Since the arrow is motionless at every instant and since time is entirely composed of instants, this must mean that motion is impossible.
In a second “proof,” Zeno argued that the fast Achilles could not outrun a turtle given a head start. This is why. When Achilles reaches the starting point of the turtle, the turtle has moved a little bit forward. It will then take Achilles some additional time to run that extra distance, by which time the turtle will have moved a bit forward once more. This reasoning can be continued ad infinitum, and as a consequence, Achilles will never overtake the turtle (see Fig. 283). Zeno thus concluded that it is impossible to talk sensibly about motion, so it was better to drop the concept altogether.
Fig. 283 – One of Zeno’s paradoxes. Achilles can never overtake a turtle, because each time Achilles reaches the previous position of the turtle, the turtle has moved a little to the right. This can be repeated ad infinitum. (Martin Grandjean, CC BY-SA 4.0)
Despite the flaws in these arguments, it is remarkable that both Parmenides and Zeno were willing to follow logic and reason, even when it ran counter to both conventional wisdom and basic experience. This, too, became a hallmark of science.
Another radical new theory about the building blocks of the universe came from the philosophers Leucippus (5th century BC) and his pupil Democritus (c. 460–370 BC). They believed that everything in the world is made up of indivisible and indestructible particles, which they called atoms (meaning “uncuttable”). Democritus wrote:
Bitter and sweet are opinions. Color is an opinion. In truth, there are only atoms and the void.
These atoms had different shapes, could bounce off each other and get stuck together in different combinations, explaining the different physical phenomena in the world. For instance, Democritus believed that bitterness was caused by small, angular atoms passing across the tongue, whereas sweetness was caused by larger, smoother atoms. Water atoms are smooth and slippery, while salt atoms are sharp and pointed, and iron atoms have strong hooks that lock them into a solid. Democritus also believed we can see the world because sheets of atoms, which he called eidola, are released by objects. These sheets then pass through the air and into our eyes.
Since he believed there were an infinite amount of atoms, there must as a consequence also be an infinite amount of worlds. He then added that it was a matter of chance (“tykhe”) whether any of them could sustain life. He seems to have been the first philosopher to give an important role to chance.
Again, it is easy to assume that Democritus was an atheist, but this was not the case. In fact, he believed the gods were made from atoms as well. He claimed they could be seen during sleep, when divine eidola penetrate our bodies. Peculiarly, he seems to have believed that these eidola were not emitted by gods (as in the case of ordinary objects), but actually were gods themselves, although not much is known about his thoughts on the matter.
No matter how inventive and creative the theories of the pre-Socratics were, they still had no method to discover which of them (if any) was correct. Overstating their faith in reason, they rarely bothered to corroborate their philosophical claims with empirical evidence. Without evidence, however, these theories are little more than fantasies of the human mind. The theory of atoms, however, turned out correct. Today we can see them individually with scanning tunneling microscopes (see Fig. 284).
Fig. 284 – Atoms as seen through a scanning tunneling microscope.
Thales is also considered to be the first true mathematician. Since the early days of Sumer, simple arithmetic had been used for practical purposes, such as construction projects, and in India, some remarkable mathematical reasoning was used for the construction of altars. In Greece, however, mathematicians started to study math for its own sake. They also constructed formal proofs to demonstrate the validity of mathematical theorems, instead of only giving numerical examples to make their theorems plausible.
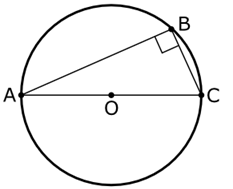
Later Greek writers attributed to Thales the discovery of a proof for what is now called Thales’s theorem. In modern vocabulary, it reads:
If points A, B, and C are points on a circle and the line AC is the diameter of the circle, then the angle at point B is always 90 degrees, no matter where point B is located on the circle (see Fig. 285).
Fig. 285 – Thales’ theorem.
The Babylonians had already empirically discovered this theorem, but Thales set out to prove it with absolute certainty. Let’s go through his reasoning.
We first have to show that the combined angles of a triangle are 180 degrees. To do this, we take a triangle of arbitrary shape and call its angles a, b, and c (see Fig. 286). Next, we draw two additional triangles of the exact same shape and place them as shown in the image. At the place where the three triangles intersect, we see that the angles a, b, and c add up to a straight angle of 180 degrees. Since the initial triangle also has angles a, b, and c, we have now found that these angles indeed add up to exactly 180 degrees. Notice that we started with an arbitrary triangle. We could do the same procedure for every triangle imaginable. So, we have discovered that all triangles have angles that add up to exactly 180 degrees.
Fig. 286 – Diagram to proof the combined angles of a triangle are 180 degrees
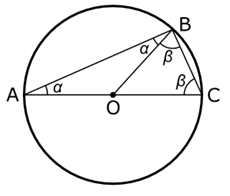
Fig. 287 – Geometric construction used to proof Thales’ theorem
Next, we look at Fig. 287, where Thales drew an extra line, OB. Since the lines AO, BO, and CO are all radii of the circle, they are of equal length. Since the triangle ABO has two equal sides, it must mean that the angles α must also be equal. The same goes for triangle BCO and the angles β.
Since the combined angles of a triangle are 180 degrees, we find for triangle ABC:
By dividing both sides by two, it must be true that:
Since the angle at point B consists of angles α and β, it must be equal to 90 degrees. This proves Thales’s theorem.
The certainty of this type of reasoning is unique to mathematics. Since every step of the argument is logically indisputable, it must mean that the conclusion is not merely an opinion, but necessarily true. The fact that the human mind is able to derive such abstract truths with absolute certainty mesmerized the Greeks. In fact, for some, these results were considered sacred. For instance, Ptolemy, who used mathematics to obtain a “certain and steadfast” model of the solar system (which we will discuss near the end of this chapter),
believed that the “constancy, order, symmetry, and calm” of mathematics is “associated with the divine” and “makes its followers lovers of divine beauty.”
Pythagoras (580–500 BC), the most famous early mathematician, was born on the Island of Samos, close to Miletus. He was credited by later Greek authors with a whole list of inventions, but little is actually known about his teachings. Greek sources do agree that Pythagoras was an ascetic who founded a sectarian school where students lived together and were sworn to secrecy. New initiates of the school were not permitted to see Pythagoras until after they had completed a five-year initiation period. Instead, they could listen to him lecture from behind a veil while they remained completely silent. The sources also claim that Pythagoras was a strict vegetarian, believed sex weakened the soul, and did not approve of writing. He also believed in reincarnation and even claimed to remember his past lives. Based on his belief in this “Indian” concept, a 3rd century AD Greek writer even claimed Pythagoras had studied under Hindu sages in India, but most historians do not consider this likely.
Later Greek authors attributed to Pythagoras the discovery of a proof for what is now known as the Pythagorean theorem. The theorem itself (without the proof) had been known earlier. The Babylonians and the Egyptians had used the Pythagorean rule for over a thousand years, and the Indian mathematician Baudhayana, between 800 and 600 BC, was the first to explicitly state the theorem (but saw no need to prove it). The Chinese book Zhoubi Suanjing seems to offer a proof of the Pythagorean theorem for a triangle with lengths 3, 4, and 5 (if we are not reading too much into some unclear passages). The text is attributed to Shang Gao, the astronomer of the Duke of Zhou (11th century BC), which predates Pythagoras by about 500 years, yet the date of the proof is unsure as various parts of the book have been updated over later centuries, some even in the first two centuries AD. A commentator from the 3rd century AD added Fig. 289 to the text, which is a geometric figure that can be used to prove the theorem and seems to be the figure described in words in the older text.
Fig. 288 – Pythagoras (Paolo Monti, CC BY-SA 4.0)
Fig. 289 – A diagram Zhao Shuang added in the 3rd century AD to the Zhoubi Suanjing that can be used to prove the Pythagorean theorem
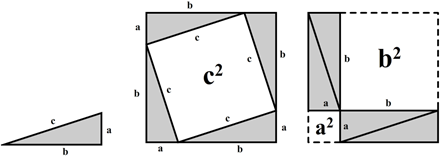
The most accessible proof of the Pythagorean theorem is depicted in Fig. 290. On the left, we see an arbitrary triangle with one angle of 90 degrees. In the second image, four of these triangles are arranged to form a square. The white square in the middle now has an area equal to c2. In the third image, we have rearranged the triangles, revealing two white squares with areas a2 and b2. Since the white areas in both arrangements must be equal, we find the Pythagorean Theorem:
Fig. 290 – Geometric construction used to prove the Pythagorean theorem
Pythagoras is also credited with the discovery of the mathematical basis of music. According to legend, Pythagoras made his discovery by listening to the different sounds of blacksmith hammers. He noticed that some hammers, when struck together, created a harmonious sound, while others didn’t. Pythagoras discovered the hammers sounded well together if their weight ratios could be described by small integers. For instance, the ratio of 2:1 sounded good, corresponding to a difference of an octave. A ratio of 3:2 gives us a difference of a perfect fifth and a ratio of 9:8 corresponds to a difference of one whole tone. He therefore concluded that musical harmony could be described by mathematical ratios. Curiously, actually performing this experiment with hammers does not yield these results. We do obtain these ratios, however, when using strings. If we cut the length of a string in half, for instance, we get double the frequency, which corresponds to an increase of one octave.
The discovery of the mathematical nature of music gave Pythagoras the idea that perhaps the entire universe is governed by mathematics. Aristotle later wrote that “the Pythagoreans constructed the whole universe out of numbers.” Pythagoras himself concluded:
World is number.
Numbers, according to Pythagoras, were the fundamental building blocks of the universe and were therefore deemed divine. Pythagoras was specifically impressed by the tetractys, which consists of ten points arranged in rows of one, two, three, and four points and which together form a triangle (see Fig. 291).
Fig. 291 – The tetractys
A prayer of the Pythagoreans shows the importance of the tetractys:
Bless us, divine number, you who generated gods and men! O holy, holy Tetractys, you that contains the root and source of the eternally flowing creation! For the divine number begins with the profound, pure unity until it comes to the holy four; then it begets the mother of all, the all-comprising, all-bounding, the first-born, the never-swerving, the never-tiring holy ten, the keyholder of all. [110]
Pythagoras also applied his theory of numbers to the motion of the planets, which he assumed could be explained by the same mathematical ratios as his musical instruments. He even took the analogy further. He claimed the planets move in spherical concentric shells, which created harmonious sounds, inaudible to the human ear. He called this the harmony of the spheres. According to Aristotle, this was the first physical model of the universe ever proposed. Anaximenes added to this model the idea that the stars were all stuck to a crystalline sphere, which rotated once every 24 hours. This idea seems ludicrous from a modern standpoint, but sounded reasonable at the time, given that all stars seem to move in unison around the Earth every 24 hours, with the distances between the stars kept constant. In reality, of course, the daily motion of the stars is only apparent, and is instead caused by the Earth rotating around its own axis.
Pythagoras’s theorem that the whole universe can be explained in terms of (whole) numbers came under threat when Hippasus (c. 530–450 BC), one of his students, discovered irrational numbers (although some sources credit Pythagoras himself). An irrational number is a number that cannot be expressed as a fraction of integers (such as 3/8 or 1/10). The first irrational number they stumbled upon was √2. When taking a right triangle where both a and b have a length of 1, the resulting side c has to be equal to √2. Horrified by the realization that this number cannot be described in whole numbers, Pythagoras wanted to keep the discovery a secret. One day, however, Hippasus revealed the secret and was murdered by the sect as a result.
The most accessible proof of the existence of irrational numbers uses the famous method of proof by contradiction[4]. In trying to prove that √2 is an irrational number, we set out assuming just the opposite: that √2 is a rational number. If this assumption leads to a contradiction, it must mean that √2 is an irrational number.
If √2 is a rational number, we must be able to express it as a fraction of the form a/b, where a and b are integers:
Squaring both sides of the equation, we find:
This can be rearranged algebraically into:
Since a number multiplied by 2 always gives an even number, this must mean a2 is necessarily even. Since the square of an even number is always even, this must mean that a is also necessarily even. Since a is even and since the smallest even number is 2, this must mean that a2 is always a multiple of 4. According to the formula a2 = 2b2, this must mean that b2 is a multiple of 2, and this makes b necessarily even. And here comes the trick. It is always possible to simplify a fraction so that at least a or b will be odd (for instance, we can simplify the fraction 4/10 to 2/5). We have now found that a and b are both even and that one of them is necessarily odd. This cannot both be true. Therefore, we must conclude that our assumption that √2 is a rational number must be false. Therefore, √2 is an irrational number.
The classical Greeks were captivated by their mathematical discoveries, which they also expressed in their architecture. Take, for instance, the famous Temple of Hera from around 500 BC, which, to this day, is a symbol of symmetry, mathematical harmony, and beauty (see Fig. 292).
The finest example of Greek architecture is the temple of Athena Parthenos (“Athena the Virgin”), also known as the Parthenon, which was built between 447 and 438 BC on the top of the Acropolis in Athens (see Fig. 293 and Fig. 294). Here, the obsession with mathematical perfection was pushed to the extreme. A mathematical ratio of 9:4 was used throughout the temple. This ratio is found in the relationship between the width and height of the temple, between the width and length of the temple, and in the space between the columns as compared to their diameters. To the Greeks, these exact mathematical relationships signified beauty and harmony.
Fig. 292 – The Temple of Hera (c. 500 BC) (Norbert Nagel, CC BY-SA 3.0)
Fig. 293 – The Parthenon (447 – 438 BC) (Steve Swayne, CC BY-SA 2.0)
Fig. 294 – The Parthenon on top of the Acropolis (447 – 438 BC). On the inside, Pheidias (c. 480 – 430 BC), the most famous sculptor of Greece, added a colossal sculpture of the goddess Athena wrought in gold and ivory. (© Shutterstock)
But there is more. Some experts believe that various sides of the Parthenon are curved to correct for the curvature caused by perspective. In Fig. 295, this effect is highly exaggerated to make it more visible. The base and the roof arch upwards, the columns tilt inwards, and the diameter of the columns and the spaces between the columns are shorter near the corners. As a result, the building appears even more geometrically perfect.
Fig. 295 – Exaggerated view of the deliberate curvature of the Parthenon (Napolean Vier, CC BY-SA 3.0)
Around 300 BC, the Greek mathematician Euclid systematized mathematics in his thirteen-part masterpiece called The Elements. Euclid took all the mathematical proofs that had been discovered so far and connected them together into a coherent system. In this process, he discovered that all known statements in geometry could be logically derived from just five axioms (“things we can take for granted”). These axioms, in turn, were so self-evident that no right-thinking person would doubt their validity. The axioms are:
I. Two points can be connected by a straight line.
II. A finite line can be lengthened into an infinitely long line.
III. A finite line can be the radius of a circle.
IV. All right angles are equal to one another.
V. Only parallel lines never intersect.
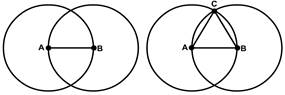
Surprisingly, the whole of geometry can be derived from these five simple statements. Let’s discuss a simple example. In Euclid’s first proposition, he showed how to create an equilateral triangle (a triangle with equal sides) from his axioms. On the left side of Fig. 296, we see a line drawn from A to B (axiom I). With a compass, we can make this line the radius of two circles of equal size (axiom III). On the right side of the figure, we have added point C, where the two circles intersect. Since lines AB, BC, and CA are all radii of one or both of the circles, they must be of equal size, and triangle ABC is, therefore, exactly equilateral.
Fig. 296 – Drawing used to proof Euclid’s first proposition
Fig. 297 – Archimedes found pi up to five decimal places, by approximating a circle by a polygon of progressively more sides.
In proposition 47, Euclid famously showed how to prove the Pythagorean theorem from his axioms.
The greatest mathematician of the ancient world was Archimedes (c. 287–212 BC). His inventions are many. He managed to find pi to five decimal places, by approximating a circle by a polygon of progressively more sides (see Fig. 297). He then used pi to calculate the area of a circle, an ellipse, and a parabola, and the volume of a sphere, a cylinder, and a cone. In a work called The Sand Reckoner, he made an estimate of the amount of sand it would take to fill the universe. At the time, the assumption was that the universe was about 10,000 Earth diameters wide, which, Archimedes calculated, can be filled with 1064 grains of sand.
Archimedes also had great practical skills. It is said he made machines that aided the Greeks at war, including a pulley system to lift enemy ships out of the water. He also understood the principle of the lever. The longer the arm of a lever, the lower the force required to lift an object. If long enough, a lever can be used to lift objects of any weight. He therefore claimed, “give me a place to stand, and I will move the Earth.” He was also asked by the king of Syracuse to figure out whether his crown was made of pure gold or whether it was a mixture. It is said that he figured out how to solve the problem when stepping into an overfilled bath. The water that overflowed, he realized, was equal to the volume of his body. This experiment could be repeated to find the volume of the crown. Comparing the weight of the crown with a piece of pure gold of equal volume, he should be able to find out if the crown was made of pure gold. It is said that when he found the answer, he jumped from his bath and ran naked through the streets shouting “eureka” (“I found it”).
Both Euclid and Archimedes studied in the great library of Alexandria, which was founded around 300 BC by the Macedonian king of Egypt, Ptolemy I Soter (c. 367–282 BC), a former general of Alexander the Great (356–323 BC). The purpose of the library was to collect all the important texts in the known world. The library housed an estimated 100,000 scrolls. Associated with the library was a community of scholars, who resided in the Musaeum, named after the Muses, the goddesses who inspire the arts and the sciences. In one of the greatest traumatic events ever to hit philosophy, the library unintentionally went up in flames when Caesar invaded in 48 BC. According to legend, the documents that survived were finally burned by Caliph Omar in 640 AD, who claimed their content heretical. It was said he used the scrolls to heat public baths for nearly six months.
The philosopher Plato (c. 425–348 BC) was highly influenced by Pythagoras. He was inspired by his belief that numbers were the foundation of the universe, and he was attracted to the absolute certainty inherent in mathematics. It was for this reason that the sign above the entrance of his school, the Akademia, read:
Let no one ignorant of geometry enter here.
Fig. 298 – Mosaic of Plato’s Academy from Pompeii (100 BC – 100 AD) (Jebulon; Museo Nazionale Archeologico, Naples)
Plato’s most important contribution to philosophy was his doctrine of the Forms (also called the doctrine of Ideas). According to Plato, the world of appearances (the world we see around us) was imperfect and subject to change, yet at the base of every object, there existed an ideal, eternal, and unchanging Form. These Forms, he believed, existed in an objective reality in a dimension higher than the material world. He called this reality the world of Forms.
In his Timaeus, Plato hypothesized that the world was created by a Divine Craftsman (demiurge), who created the universe by giving shape to already existing unformed matter using geometry. He believed that the Divine Craftsman had fashioned matter first into regular triangles and then combined them into the five Platonic solids (see Fig. 299). A Platonic solid is a polyhedron consisting of identical polygonal faces with equal sides and angles. Plato was impressed by the fact that only five of such solids exist, and he believed that they were the building blocks of five elements: water, earth, fire, air, and a heavenly element.
Fig. 299 – The Platonic solids by Kepler (1597) (Harmonices Mundi)
Fire, Plato believed, must be made of the pointy tetrahedrons since it feels sharp. Air must be made of the octahedrons since it is so smooth that one can barely feel it. Water must be made of icosahedrons since it easily flows out of our hands when we try to pick it up. Earth must be made out of hexahedrons since earth is tough and clumsy. The fifth Platonic solid, the dodecahedron, Plato claimed, “God used for arranging the constellations on the whole heaven.” His student Aristotle would later also identify five elements (calling the fifth one “ether”), although he had no interest in connecting them to the Platonic solids.
From these elements, the demiurge created material objects based on the Forms, in the same way a builder uses a blueprint. Matter, however, can never match the Forms perfectly, which explains the difference between the world of Forms and the world of appearances. Yet, since objects still resemble the Forms by approximation, we can use reason to deduce what the underlying Forms must be like. A great example is the triangle. Nowhere in the universe will we ever find a perfect mathematical triangle, yet our mind is capable of deducing this concept after seeing many imperfect triangles on Earth.
Surprisingly, some mathematicians and physicists to this day call themselves Platonists, as they believe that the everyday world of appearances can be fully explained by an unseen world of mathematical relationships and numerical constants.
According to Plato, understanding these Forms comes so naturally to us that knowledge of them must already be inside of us. As a believer in reincarnation, he claimed that we must have known about them in a previous life but have since forgotten about them. To know the Forms, therefore, we don’t need to discover them but only recollect them. We read:
[The soul has] seen all things here and in the underworld. There is nothing which it has not learned, so it is in no way surprising that it can recollect the things it knew before. [111]
For instance, how do we distinguish between a river and, say, a lake? According to Plato, this is possible because we inherently know the Form of a river in our minds. For his student Aristotle, the concept of a river forms by making generalizations after seeing many rivers, but for Plato, it was more than that. He believed that the Forms had an independent existence.
The soul, Plato claimed, also preexisted in the world of Forms, and must therefore be immortal. In a complete reversal from the shades in the Homeric underworld, who were nothing without their body, Plato stated that “what gives each one of us his being is nothing but his soul, whereas the body is no more than a shadow which keeps us company.” It is now “the real man—the undying thing called the soul” that departs after death. Plato then lets Socrates explain that after death, true sinners go to Tartarus either for a year or forever, those with limited sins go for purification to the Acherusian Lake, while those who have “purified themselves sufficiently by philosophy live thereafter altogether without bodies.” [112]
In his Myth of Er, in his Republic, Plato recounted a myth of a slain warrior named Er, who after death sees divine judges send souls either through a hole in the sky or down in a hole in the earth, depending on whether they were just or unjust. In heaven, their good deeds were rewarded and in hell their sins were punished. After a thousand years, the souls return to Earth for new incarnations, either as humans or as animals. Before entering their new bodies, they would drink from the River of Forgetfulness, causing them to forget their previous lives.
When discussing these stories, Plato made sure to tell us they are just myths, not to be taken too literally. But in his view, they can’t be too far off:
Of course, no reasonable person ought to insist that the facts are exactly as I have described them, but that either this or something very like it is a true account of our souls and their future habitations. [112]
This idea of an eternal soul would later appeal to Jews and Christians, as did the idea of a perfect spiritual reality completely disjoint from the material realm. In a text called the Wisdom of Solomon (1st century BC), the idea of an eternal soul made its way into Judaism, which before this point had no real notion of an afterlife (ironically, the same text then rails against the influence of Greek culture on Israel). Augustine (354–430), the influential Christian saint, explicitly recognized the similarities between Christianity and Plato’s teachings, stating the Platonists come “closest to us”.
Fig. 300 – Copy of a bust of Plato by Silanion (c. 370 BC) (Marie-Lan Nguyen, CC BY 2.5; Capitoline Museum, Italy)
Fig. 301 – Roman copy of a bust of Aristotle by Lysippos (c. 330 BC) (Jastrow; Museo nazionale romano di palazzo Altemps, Italy)
The most influential thinker of ancient Greece was Plato’s greatest student, Aristotle (384–322 BC), founder of the Lyceum, another Athenian school of philosophy. Aristotle was a pioneer of great genius, on the level of Newton and Einstein. He made world-changing contributions in many fields, which we will discuss in this and various later chapters. The works of Aristotle that remain are the instruction books for his students, which can be quite dry, as academic works often are. Aristotle also wrote public works in dialogue form, which were praised in ancient times for their eloquence, but they have since been lost.
Unlike any other thinker in the ancient world, Aristotle valued empirical evidence, making him the grandfather of science. Aristotle claimed that Plato, with his abstract speculation about an unmeasurable reality of Forms, had neglected the study of nature. True knowledge, Aristotle claimed, was gained by observing similarities in the phenomena around us and making generalizations based on these observations. According to Aristotle, this was all there was to it. He saw no need for a metaphysical world of Forms in his description of the world. In the Nicomachean Ethics, he writes how he dealt with this crucial disagreement with his friend and teacher, Plato:
But perhaps it is desirable that we should examine the notion of a Universal Good [the Form of the Good], and review the difficulties that it involves, although such an inquiry goes against the grain because of our friendship for the authors of the Theory of Ideas [Forms]. Still perhaps it would appear desirable, and indeed it would seem to be obligatory, especially for a philosopher, to sacrifice even one’s closest personal ties in defense of the truth. Both are dear to us, yet it is our duty to prefer the truth. [113]
According to Aristotle, objects did have a “form” with a small “f” (their shape), but since this form was never observed apart from the object itself, he felt little reason to assume that forms had a separate existence in a more abstract world. This was even true for the soul, which he claimed could not exist without the body and therefore could not be immortal (yet, in one curious passage he deviates from this opinion and states that part of the soul was immortal after all).
Aristotle exposed the theory of the Forms as absurd, as it runs into problems in abstract cases. Take for instance a walk from point A to point B. Does the line of the walk exist as a Form separate from the walk? And if it exists, where would that line be located? According to Aristotle, these questions are nonsensical.
Finally, Plato had claimed that the Forms were eternal and unchanging, but could not explain how they introduced change into the world. Plato tried to address this problem by stating that objects in the real world were not identical to the forms, but only “participated” in them. Aristotle rightly countered that this explained nothing, calling Plato’s explanation mere “empty words and poetical metaphors.” [109]
Instead of focusing on the world of forms, Aristotle spent most of his time concentrating on the world that lies within our grasp. For example, he became the first biologist. He dissected animals and plants to understand how they functioned and broke eggs at various levels of development to chart the growth of the chick embryo.
Although these biological studies made him the grandfather of science, Aristotle did not do experiments in the modern sense. The word he used instead was observation (pepeiramenoi). He simply observed the world but generally did not design experiments with the sole purpose of isolating a phenomenon and manipulating it in order to discover how it works.[5] His lack of experimentation famously showed when he wrote that heavy objects fall faster than light objects. This might sound recognizable from our day-to-day experience (a lead ball falls faster than a sheet of paper), but a simple experiment can show both objects hit the ground at the same time when air friction is small (crumple the paper into a ball to reduce air friction and both objects will fall at the same rate).
The Greek who came closest to being a modern scientist was likely Ptolemy (c. 100–170 AD). In his Optics, he described the use of a piece of equipment containing a bronze disk, metal mirrors of various shapes, and a sighting tube. With this experimental setup, he demonstrated very accurately that the angle of incidence of a light ray hitting a mirror is equal to the angle of reflection. He also conducted an experiment on refraction, which involves a change in the direction of light when it propagates from one substance to another (for instance from air to glass), but here he found an erroneous result, likely because he was fudging with his own data to make it fit his hypothesis.
Aristotle also created the most sophisticated theory of the elements of the ancient world, which he described in his On Generation and Corruption. Aristotle hypothesized that the foundational substance of the universe was prime matter, which was a substance without any qualities. Combined with the qualities hot, cold, wet, and dry, prime matter turned into the four elements (see Fig. 302). Although his theory later turned out to be wrong, it did have remarkable explanatory power. For instance, if we give an object the qualities hot and dry, the object will catch fire. When water (with the qualities cold and wet) is heated by fire, it evaporates into air (having the qualities hot and wet).
Fig. 302 – Aristotle’s theorem of the four elements.
Aristotle also set out to classify what was necessary to fully understand a phenomenon. In his estimation, it required knowing four causes (perhaps better translated as “four explanations”). The material cause refers to the material the object is made of, the efficient cause refers to the agent that produced the object, the formal cause refers to the shape or essence of an object, and the final cause refers to the purpose (“telos”) of the object. The final cause is of particular interest here. Aristotle believed that all objects have an inherent purpose or goal. If that purpose was not yet met, it existed inherent in the object as a potentiality. For instance, oil has the potential to burn. This potentiality, Aristotle claimed, exists in the oil even when it is not burning.
Aristotle likely got this idea from his study of biology. His many years of dissecting and describing animals and plants taught him that different organs all have their own distinct function. Muscles and tendons, for example, have the purpose of moving parts of the body. The stomach has the purpose of digesting food. Seeds have the purpose (or potential) of becoming trees. This idea was finally challenged by Darwin’s theory of evolution, which showed convincingly that the perception of purpose in biology was only an epiphenomenon of natural selection (we have hearts not in order to pump blood around, but because creatures without hearts were less successful at survival).
While talking about purpose still has its place in biology, Aristotle also applied this type of thinking to material objects. For instance, he believed that the purpose of fire was to point upwards toward the stars. This is why the flame on a candle always points upwards, even when the candle is turned upside down. The purpose of the element earth was to fall down in a straight line towards the center of the universe, which he believed was located at the center of the Earth. It took 2000 years for people to realize it is not the stone that inherently “wants” to fall downward, but that the earth instead exerts a gravitational force on the stone. Aristotle’s theory, nevertheless, had remarkable explanatory power. In On the Heavens, he used it to explain the spherical shape of the earth. If matter all wants to get as close to the center of the universe as possible, you automatically end up with a spherical earth.
Aristotle wasn’t the first to believe in a spherical Earth. Plato had also written about it, but without providing evidence:
My conviction is that the earth is a round body in the center of the heavens, and therefore has no need of air or of any similar force to be a support. [114]
Aristotle did provide evidence. When the shadow of the earth falls over the moon during a lunar eclipse, the shadow is always circular. Since only a sphere creates a circular shadow from all sides, he concluded that the earth must be a sphere. Aristotle also noted that when a person travels north or south, he sees unknown stars on the horizon, which would not make sense if the earth was flat (see Fig. 303). Similarly, when a person travels either east or west, he will find that the sun rises at a different time. Finally, Aristotle noted that when a large ship sails off to the horizon, its bottom disappears first, and only later does its mast. This could be explained by assuming that the bottom of the boat becomes concealed behind the curvature of the earth (see Fig. 304).
Fig. 303 – People on different parts of a spherical Earth see different stars (S. P. Dinkgreve, worldhistorybook.com)
Fig. 304 – On a spherical Earth, the bottom of a boat can hide behind the curvature of the Earth. From a 1550 copy of On the Sphere of the World, the original dating to the 13th century.
Aristotle’s theory could also explain the motion of a falling rock. The natural motion of a stone was to move towards the center of the universe, making it fall. However, the stone can be stopped by external forces, for instance the force exerted on the rock by the floor. Aristotle saw this as an artificial or unnatural stop, which prevented the natural motion of the stone. As a result, the rock will finally lay still on the surface of the Earth.
These external forces can also explain why a rock thrown upwards continues its upward motion after leaving the hand before finally falling down again. When a rock moves upward, it leaves behind a vacuum. Since Aristotle claimed that nature “abhors a vacuum,” the surrounding air rushes in, giving the stone an extra push, propelling it upward. Eventually, though, the natural motion prevails, and the rock will fall down again.
Although incorrect, his theory was definitely consistent and the most comprehensive theory of the world thus far.
Aristotle’s four elements explained motion on Earth, but could not explain the eternal circular motion of the heavenly bodies. Why did they not fall to the center of the universe? And why did they not slow down and come to rest as objects on earth do? And why was there “no trace of change in the whole of the outermost heaven or in any one of its proper parts”? To circumvent these problems, Aristotle postulated a fifth element, called ether, from which all heavenly bodies were made, characterized by endless and unchanging circular motion.
Since the physics on earth seemed so different from the physics that governed heaven, Aristotle divided the universe into the world below the sphere of the moon and the world above the sphere of the moon. This idea of a distinct terrestrial and celestial physics was finally overthrown some 2000 years later by Isaac Newton (as will be discussed in a later chapter). Newton showed that the same gravitational force could explain both the falling of objects and the orbits of the heavenly bodies.
With his theory, Aristotle also reasoned there could not exist “more than one world,” for if there was another Earth (necessarily made of the four elements), it too would fall to the center of the universe. In the Middle Ages, this was used as an argument against aliens on other planets.
In his Metaphysics, Aristotle set out to investigate the fundamental nature of reality, which he equated with finding “the principles and causes of substances.” This investigation into substance, he claimed, went even deeper than physics. With physics we describe the natural world, but with metaphysics we want to know what it means for an object to exist in the first place. He called it the study of “being as being”. Aristotle recognized this as the First Philosophy, the study of the most foundational knowledge.
Aristotle’s metaphysics rides on the idea that every causal chain (or, perhaps more accurately: every explanation) should be finite. However, when thinking about the world, we often run into infinite regression problems. This can happen for each of the four causes:
It is impossible that one thing should come from something else as from matter [the material cause] in an infinite regress, for example, flesh from earth, earth from air, air from fire, and so on to infinity. Nor can the causes from which motion originates [the efficient cause] proceed to infinity, as though man were moved by the air, the air by the sun, the sun by strife, and so on to infinity. Neither can there be an infinite regress in the case of the reasons for which something is done [the final cause], as though walking were for the sake of health, health for the sake of happiness, and happiness for the sake of something else, so that one thing is always being done for the sake of something else. The same is true in the case of the essence [the formal cause]. [115]
To solve this problem, Aristotle began to wonder about the cause of the orbital motion of the heavenly bodies. Just like all motion, Aristotle believed, it was in need of a mover (an efficient cause). This mover, however, had to “move without being moved,” for otherwise, it would itself also be in need of a mover (creating infinite regression). He therefore called it the “unmoved mover,” the “uncaused cause,” or the “first cause.” But how can something move something else without itself moving? According to Aristotle, the only solution was to assume that the unmoved mover was an object of desire, “producing motion by being loved.” Just as a bottle of water can “cause” a thirsty person to move towards it, so too are the heavenly bodies compelled into orbit by the unmoved mover. It is the final cause (or purpose) of the heavenly bodies to move as the unmoved mover desires. To avoid infinite regression, Aristotle then claimed that every motion on earth is (somehow) causally linked in a finite number of steps to the motion of the heavenly bodies, which in turn was caused by the unmoved mover.
Aristotle equated his unmoved mover with God, making his metaphysics a theological endeavor. He then set out to use reason to derive the characteristics of this god. First of all, since all matter can be brought into motion, but the unmoved mover cannot, it follows that the unmoved mover must be immaterial. With reason being the highest quality in the universe, he claimed God must be the supreme thinker, and being a thinker, he claimed his god must be alive. But what does the supreme thinker think about? Being the perfect thinker, it has to think about itself. Finally, Aristotle had to figure out whether there was just one unmoved mover, or whether there were more of them. He had reason to believe there were more, as Eudoxus—another student of Plato—had identified 27 different circular motions in the heavens, perhaps requiring 27 gods (more on this later). Aristotle finally settled on one unmoved mover, believing God was indivisible.
One last clarification is necessary. In modern times, we often envision a first cause to occur at the beginning of the universe and for everything to unfold from there. Aristotle, however, believed in an eternal universe, since he believed the heavenly bodies had existed unchanged for all eternity. So, his unmoved mover was not the first cause at the beginning of time, but instead compelled the heavenly bodies forward at every moment in time. Without the unmoved mover, he believed, the planets would stop.
Aristotle also laid the foundation of formal logic in a work called the Organon, which consists of six books on the topic. The goal of this pursuit was to figure out how we can attain reliable knowledge. In his book Prior Analytics, he discussed what logical inferences could be made with absolute certainty from various simple statements. Take, for instance, the following sentence: “All ravens are black.” If we regard this statement as true, then we can with absolute certainty infer that the following statement must also be true: “There are no white ravens.” Aristotle called this deductive reasoning. He defined deduction (sullogismos) as follows:
A deduction is an argument in which, certain things having been supposed, something other than what was laid down results by necessity because these things are so. By “because these things are so” I mean that they result through these, and by “resulting through these” I mean that no term is required from outside for the necessity to come about. [116]
The “things supposed” are the premises (protasis) of the argument, while what “results by necessity” are the conclusions (sumperas-ma).
To systematize his thinking, he created four generalized statements:
I. All X are Y
II. No X are Y
III. Some X are Y
IV. Some X are not Y
To reason correctly with these statements, Aristotle defined three self-evident axioms:
I.
The law of identity
Words either mean the same thing or they don’t.
II.
The law of contradiction
A statement can’t both be true and untrue at the same time.
III.
The law of the excluded middle
A statement is always either true or not true. There is no third option.
These simple ideas, often called the three laws of thought, are still used in philosophy, mathematics, and computer programming.
Aristotle then showed how to combine different statements to find new conclusions. He called such a construction a syllogism. Let’s study an example:
Statement 1 All X are Y
Statement 2 All Z are X
Conclusion Therefore, all Z are Y
That this conclusion follows is often easier to understand by filling in words for X, Y, and Z. For example:
Statement 1 All Greeks are mortal
Statement 2 All Athenians are Greek
Conclusion Therefore, all Athenians are mortal
When trying all combinations, he found there are 256 possible syllogisms, of which only 24 turned out true. Here we find two other examples of correct syllogisms:
Statement 1 All X are Y
Statement 2 Some Z are X
Conclusion Therefore, some Z are Y
Statement 1 No X is Y
Statement 2 All Z are X
Conclusion Therefore, no Z are Y
In his Posterior Analytics, Aristotle discussed a crucial problem with syllogistic reasoning. In themselves, syllogisms tell us nothing about the world. The conclusions are only true if the premises are shown to be true in the first place. Yet, in most cases, we cannot prove the premises with absolute certainty. Take, for instance, the premise “All ravens are black.” Although all ravens discovered thus far have been black, there is no way to know for sure whether they are all black. To prove that “all ravens are black,” we therefore cannot rely on deduction and have to rely on the next best thing: induction (epagoge). Induction works by making generalizations about the world based on a finite number of measurements. Aristotle called it “an argument from the particular to the universal.” If we find enough particular ravens and they are all black, we can convince ourselves of the universal statement “All ravens are black,” but we can never be completely certain.
Aristotle then went further, claiming that these two methods—deduction and induction—are the only reliable paths to knowledge. When we are born, he claimed, our mind is like an “unscribed tablet.” At this point, our mind contains no innate knowledge, but merely the capacity to know. Anticipating the scientific revolution that would occur two millennia after his death—making Aristotle the greatest genius of all time—he claimed that all knowledge had to enter the mind through the senses:
We conclude that […] knowledge [is] neither innate in a determinate form, nor developed from other higher states of knowledge, but from sense-perception. [117]
In the Middle Ages, Saint Thomas Aquinas (1225–1274) summarized his position very concisely:
Nothing is in the intellect that was not first in the senses.
Through sensory observation, Aristotle claimed, we can in turn apply induction to discover the first principles of science. The rest of science should then follow by syllogistic deduction.
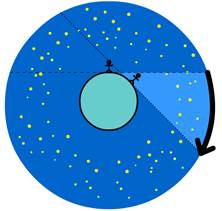
Eratosthenes (c. 276–195 BC) found a way to determine the circumference of the earth. He noticed that at a certain longitude and at a certain time of the year, the sun would be directly overhead. As a result, sunlight would shine directly into a well, leaving no shadow at the bottom. At this exact same time, a lighthouse situated hundreds of kilometers north did create a shadow (see Fig. 305).
Fig. 305 – The method used by Eratosthenes to calculate the circumference of the earth (S. P. Dinkgreve, worldhistorybook.com)
The figure shows that the angle of the shadow is equal to the angle depicted at the center of the earth (in mathematics, we call these alternate angles). Eratosthenes measured the angle of the shadow to be 7.2 degrees, which corresponds to 1/50th of the earth’s circumference. Multiplying the distance between the well and the lighthouse by 50, he found a circumference only one percentage point removed from the modern value of 40,000 kilometers. Eratosthenes also calculated the angle of the Earth’s axis at 23.3 degrees and introduced the idea of a leap day to even out the calendar.
Aristarchus (c. 310–230 BC) used the circumference of the earth and the size of the earth’s shadow on the moon to calculate the distance to the moon. With the distance to the moon, he also found a way to calculate the distance to the sun. Although both his techniques were mathematically correct, his measuring equipment was not accurate enough to find the correct answers. A few centuries later, Ptolemy managed to find out that the moon was 59 earth radii away from the earth (the modern value is 60 earth radii).
Aristarchus was also the first to propose a heliocentric model of the solar system. He showed how the rotation of the Earth’s axis could explain the apparent daily rotation of stars around the Earth and the rotation of the Earth around the sun could explain the apparent yearly rotation of the zodiac. According to Plutarch (46–119 AD) the astronomer Seleucus (2nd century BC) even had a proof of the heliocentric model, although we are not told what this proof was. Although the theory did not become widely accepted among the Greeks, Plutarch also mentioned that “Plato, when he grew old, repented that he had placed the Earth in the middle of the universe, which was not its place.”
The Greek philosophers also attempted to improve the Mesopotamian model of the solar system. It had been known since early Mesopotamian days that the planets didn’t move in simple circles across the night sky. Instead, they periodically seemed to stop, move back a little, stop again, and then move onwards again (see Fig. 306). This backward motion is called retrograde motion. The mechanism behind this motion was not understood.
Fig. 306 – The retrograde motion of Mars (S. P. Dinkgreve, worldhistorybook.com)
Plato’s faith in the geometric regularity of the world convinced him that the motion of the planets could still be understood in terms of uniform circular motion. To prove this, he famously challenged the astronomers of his day to “save the phenomena,” meaning to bring his theory of circular celestial motion in line with observed reality. This, however, turned out to be a difficult task because of the complexity of the motion of the heavenly bodies. First there was the diurnal motion, which lets all celestial bodies rise in the east and set in the west once every 24 hours (we now know this is caused by the rotation of the Earth around its axis). Then there was the annual motion, which makes the heavenly bodies rise a little earlier every day, making different constellations visible throughout the year (as caused by the motion of the Earth around the sun). Then there was the motion of the planets themselves. Both the velocity and the brightness of the planets change over time, and they also make a wavy up-and-down motion along their path within the band of the zodiac. And then, finally, there was retrograde motion.
Several people tried to solve the problem, among them Eudoxus (c. 408–355 BC), one of Plato’s students and the second-best mathematician of Greece. His mathematical works have not survived first hand, as his major proofs were incorporated into the work of Euclid.[6] Eudoxus took up the Pythagorean idea that the fixed stars were attached to a sphere, which rotates around its axis every 24 hours. The planets, in his theory, were each attached to four spheres, the first moving in the same manner as the fixed stars, the second moving the planet along the band of the zodiac, and the third and fourth spheres cleverly working together to create retrograde motion. This model, with a total of 27 spheres, brilliantly reduced the complex motion of the planets to a composite of just circular motion, in line with Plato’s challenge, but it was finally discarded because it did not account for the changes in brightness of the planets (which is caused by a change in distance).
The Greek astronomer Ptolemy, also working in the library of Alexandria, was the first to fully solve the problem. In his work called Mathematike Syntaxis, which is now known by its Arab title The Almagest (from “Al-Majisti,” meaning “the greatest”)—which is considered to be among the most influential scientific texts of all time—he produced the first accurate mathematical model describing the motion of the heavenly bodies.
Fig. 307 – Paths of the planets and the sun as seen from the earth, by James Ferguson (18th century)
Fig. 308 – Ptolemy’s model of the solar system (S. P. Dinkgreve, worldhistorybook.com)
To describe retrograde motion, Ptolemy took up an idea by the astronomer Apollonius (c. 240–190 BC). Apollonius had realized that retrograde motion could be mechanically described by assuming that the planets moved on small circular orbits, called epicycles, that were attached to a bigger orbit around the earth (see Fig. 308). He then added an idea by another great astronomer, named Hipparchus (c. 190–120 BC), who had discovered that the seasons were not exactly of equal length, suggesting the sun sped up and slowed down along its orbit. As a result, Hipparchus had claimed that the earth was not in the center of the orbit of the sun, but 1/24th the radius of the Sun’s orbit off-center. Changes in the velocity of the planets indicated that the same was true about the orbits of the planets. Finally, Ptolemy added his own invention, named the equant, which was a point in space also located slightly off center (see Fig. 308). Ptolemy masterfully showed that the center of the epicycles moved with constant velocity as seen from this point, saving Plato’s wish for uniform motion.
This model could describe all observed motions of the heavenly bodies with precision and could thus be used to make very accurate predictions of their future positions. It would remain the dominant model of the universe for 1200 years, until it was finally replaced by the heliocentric model of Nicolaus Copernicus (1473–1543 AD).
Some of the data in the Almagest seems strangely coincidental in the geocentric model but can be easily explained in the heliocentric model. For instance, the inner planets Mercury and Venus always stay close to the sun, which, we now know, is because they closely orbit the sun. Also, the outer planets all have epicycles with periods equal to one Earth year, which, we now know, is because epicycle motion is caused by the motion of the Earth around the sun. Ptolemy knew about these curious coincidences, but saw no need to explain them.
Ptolemy also wrote two other influential astronomical works. The first is the Tetrabiblos (“Four Books”), which applies his model of the universe from the Almagest to predict horoscopes. Another is the Planetary Hypotheses, in which he attempts to measure the size of the universe based on his model. To do this, he assumed that the spheres of the planets were stacked directly on top of one another and then equated the distance to the sphere of the fixed stars with the “radius of the cosmos.” His result was obviously way off, but his attempt was ambitious nonetheless.
The same Hipparchus we just mentioned also found that the stars slowly shift position, one degree every 85 years (the modern value is 72 years). He discovered this by comparing his own data with star measurements made by his predecessors about a hundred years earlier. This effect is known as precession, which occurs because the axis of the Earth is spinning like a top with a period of 26,000 years.
The Greeks also produced at least one mechanical model of the motion of the heavenly bodies, called the Antikythera mechanism, which was found in a shipwreck. The device contains 37 bronze gears enabling the device to track the movements of the moon and the sun through the zodiac (including their variable velocity). As this motion was first studied in the 2nd century BC by Hipparchus and the shipwreck dates to 70-60 BC, the device must have been built somewhere between these dates. Machines with similar complexity did not appear again until the 14th century. The device also contains some inscriptions, which mention the Saros cycle of 223 months, used to predict eclipses. All gears in the device are accounted for except one, which, according to some historians, can be used to describe the epicyclical motion of Jupiter. As it takes only a small number of gears to describe the motion of all the planets known at the time, it is also hypothesized that part of the device is missing.
Fig. 309 – The Antikythera mechanism (2nd-1st century BC) (Marsyas, CC BY-SA 2.5)
Ptolemy’s model was great at describing the motion of the planets, but there was still one problem left. Although it could describe the motions, it could not explain them. What mechanism could possibly make the planets move as circles within circles? And why was the earth not at the center as Aristotle had theorized? It would take the genius of Copernicus and Newton to finally resolve these problems.
